Метод расчета трехмерных координат с помощью двух плоских снимков
Введение. Применение не метрологических регистрирующих устройств (т.е. камер без внутренней системы ориентации) создает определенные трудности в использовании программного и аппаратного обеспечения, применяемого в стереофотограмметрии. В 1971 году Y.I. Abdel-Aziz, H.M. Karara (Abdel-Aziz, Y.I. , H.M. Karara, 1971) разработали метод, позволяющий применять стереофотограмметрические алгоритмы к не метрологическим камерам (т.е. камерам без фиксированного и очень точного фокусного расстояния). Этот метод получил название «прямой линейной трансформации» (в англоязычной литературе «direct linear transformation method» или DLT). Суть его состоит в том, что по двум плоским снимкам можно восстановить третью координату.
Геометрическая интерпретация метода DLT. Предположим, что точка O в пространстве имеет координату ![]() на регистрирующей плоскости (РП). При обработке координат с РП спроецируем точку
на регистрирующей плоскости (РП). При обработке координат с РП спроецируем точку ![]() на
на ![]() в проекционной плоскости (ПП), например, на экран монитора (рисунок 1).
в проекционной плоскости (ПП), например, на экран монитора (рисунок 1).
Обозначим оптический центр проекционной аппаратуры как N. Тогда, в инерциальном базисе XYZ, координаты точки N равны (![]() ). Координаты точки O в базисе XYZ равны (
). Координаты точки O в базисе XYZ равны (![]() ). Длина вектора
). Длина вектора![]() , соединяющего точки N и О, в базисе XYZ равна:
, соединяющего точки N и О, в базисе XYZ равна: ![]() =[
=[![]() ].
].
Добавим в ПП третью ось W и направим её ортогонально проекционной плоскости. Тогда в проекционной плоскости имеем систему координат VUW. Точка O, обладающая в инерциальном базисе XYZтремя координатами (![]() ), в базисе VUW
), в базисе VUW![]() ПП будет иметь координаты I=[
ПП будет иметь координаты I=[![]() ] (рисунок 1).
] (рисунок 1).
Обозначим центр проекционной плоскости буквой Pи запишем для него координаты в базисе VUW как P=[![]() ].
].
Оптический центр проекционной аппаратуры Nв базисе VUW имеет координаты: N=[![]() ].
].
Вектор![]() , проведенный из точки N в точку I относительно центра ПП (точкаP) имеет следующие координаты:
, проведенный из точки N в точку I относительно центра ПП (точкаP) имеет следующие координаты: ![]() =[
=[![]() ] (рисунок 1).
] (рисунок 1).
Точки O, I и N коллинеарные, т.е. лежат на одной прямой, следовательно, длину вектора ![]() можно выразить как:
можно выразить как: ![]() =
=![]() *
*![]() , где
, где ![]() — масштабирующий фактор.
— масштабирующий фактор.
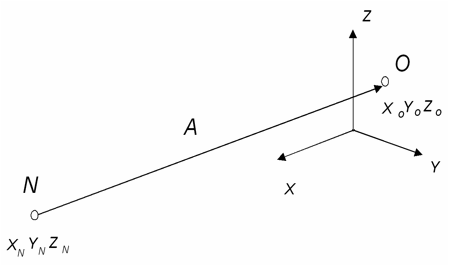
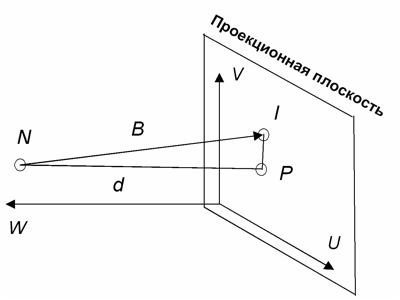
Рисунок 1 – Верхний рисунок — проекция оптического центра О на проекционную плоскость (пояснения в тексте). Нижний рисунок – система координат, применяемая в методе DLT. XYZ– инерциальный базис; UVW – система координат камеры; N – оптический центр камеры; P- проекция оптического центра на проекционную плоскость; I– искомая точка
Поскольку вектор ![]() имеет трехмерные координаты, то спроецируем его на ПП через матрицу направляющих косинусов:
имеет трехмерные координаты, то спроецируем его на ПП через матрицу направляющих косинусов:
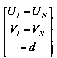 =
=![]()
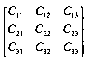 *
*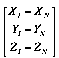 (1)
(1)
где ![]() — направляющие косинусы или
— направляющие косинусы или
![]() =
=![]()
![]() =
=![]() (2)
(2)
-d=![]()
Из уравнений (2) найдем масштабирующий коэффициент![]() :
:
![]() =
= ![]() (3)
(3)
Подставляя уравнение (3) в уравнения (2) получим, что
![]() =
=![]() (4)
(4)
![]() =
=![]()
При обработке видеоизображения ![]() координаты точки O в масштабе видеоснимка (например, экран монитора) рассчитываются в точках экрана – единицах, отличных от метрической системы. Следовательно, необходимо ввести поправочные коэффициенты
координаты точки O в масштабе видеоснимка (например, экран монитора) рассчитываются в точках экрана – единицах, отличных от метрической системы. Следовательно, необходимо ввести поправочные коэффициенты ![]() и
и ![]() ,трансформирующие точки экрана в метрическую систему координат:
,трансформирующие точки экрана в метрическую систему координат:
![]() =
=![]() *
*![]()
![]() =
=![]() *
*![]()
![]() =
=![]() (5)
(5)
![]() =
=![]()
Действительные координаты точки O в базисе XYZ можно выразить через координаты ![]() и
и ![]() базисавидеоснимкаVUW следующим образом:
базисавидеоснимкаVUW следующим образом:
![]() =
=![]()
![]() =
=![]() , (6)
, (6)
где ![]() =
=![]() ;
; ![]() =
=![]() ;D= —
;D= —![]() ;
;
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ;
;
![]() =
=![]()
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]()
Коэффициенты ![]() —
—![]() в уравнении (6) называются коэффициенты прямой линейной трансформации.
в уравнении (6) называются коэффициенты прямой линейной трансформации.
В уравнения (6) можно добавить ошибки, связанные с отображением реальных координат на видеоснимке, например, оптические искажения (![]() и
и ![]() ). Тогда, уравнения DLT примут следующий вид:
). Тогда, уравнения DLT примут следующий вид:
![]() =
=![]()
![]() =
=![]() (7)
(7)
где ошибки в определении действительных координат, связанные с оптическими искажениями ![]() ,
, ![]() имогут быть представлены следующим образом:
имогут быть представлены следующим образом:
![]() =
=![]()
![]() =
=![]() ,
,
где коэффициенты ![]() —
—![]() связаны с оптической дисторсией линз регистрирующей системы и видеоснимке; r,
связаны с оптической дисторсией линз регистрирующей системы и видеоснимке; r, ![]() и
и ![]() -поправочные коэффициенты. Коэффициенты
-поправочные коэффициенты. Коэффициенты ![]() —
—![]() «исправляют» ошибки действительных координат вследствие нарушения оптического центра линз.
«исправляют» ошибки действительных координат вследствие нарушения оптического центра линз.
Из уравнения (6) следует, что три действительные координаты точки О в проекционной плоскости выражаются через две координаты, т.е. два уравнения типа (6). Следовательно, из одного плоского снимка (рисунок 1) нельзя получить три действительные координаты точки О (рисунок 1 нижний). Отсюда возникает потребность в создании стереопары, регистрирующей одновременно несколько точек. Количество регистрируемых точек зависит от уравнений, описывающих метод DLT. В таблице 1 представлены значения контрольных точек в зависимости от вида уравнений метода DLT.
Таблица 1 — Основные характеристики метода DLT
| Уравнение DLT |
Количество параметров в уравнении |
Минимальное число точек в тест-объекте |
|
Стандартное уравнение DLTтипа(6) |
|
6 |
|
Уравнение, учитывающее оптические дисторсии 3, 5 и 7 порядков |
|
6 |
|
|
7 |
|
|
Уравнение, учитывающее смещение центра линз |
|
8 |
Рассмотрим более подробно уравнения необходимые для определения трехмерных координат точек на тест-объекте ![]() . Обозначим их как
. Обозначим их как ![]() , где i– номер камеры; j – точки тест- объекта.
, где i– номер камеры; j – точки тест- объекта.
На одиннадцать неизвестных параметров ![]() —
—![]() приходится как минимум 12 уравнений: 6 от первой камеры и 6 от второй камеры (рисунок 2). В матричном виде решение системы уравнений (6) сводится к следующему виду:
приходится как минимум 12 уравнений: 6 от первой камеры и 6 от второй камеры (рисунок 2). В матричном виде решение системы уравнений (6) сводится к следующему виду:
X*L=Y
L=( XT*X)-1*( XT*Y), (8)
где вектор-столбец L содержит калибровочные коэффициенты ![]() —
—![]() ; X — система уравнений (7); XТ – транспонированная система уравнений (7); Y — вектор-столбец двумерных координат в плоских снимках. Особенности калибровки камер при применении метода DLT:
; X — система уравнений (7); XТ – транспонированная система уравнений (7); Y — вектор-столбец двумерных координат в плоских снимках. Особенности калибровки камер при применении метода DLT:
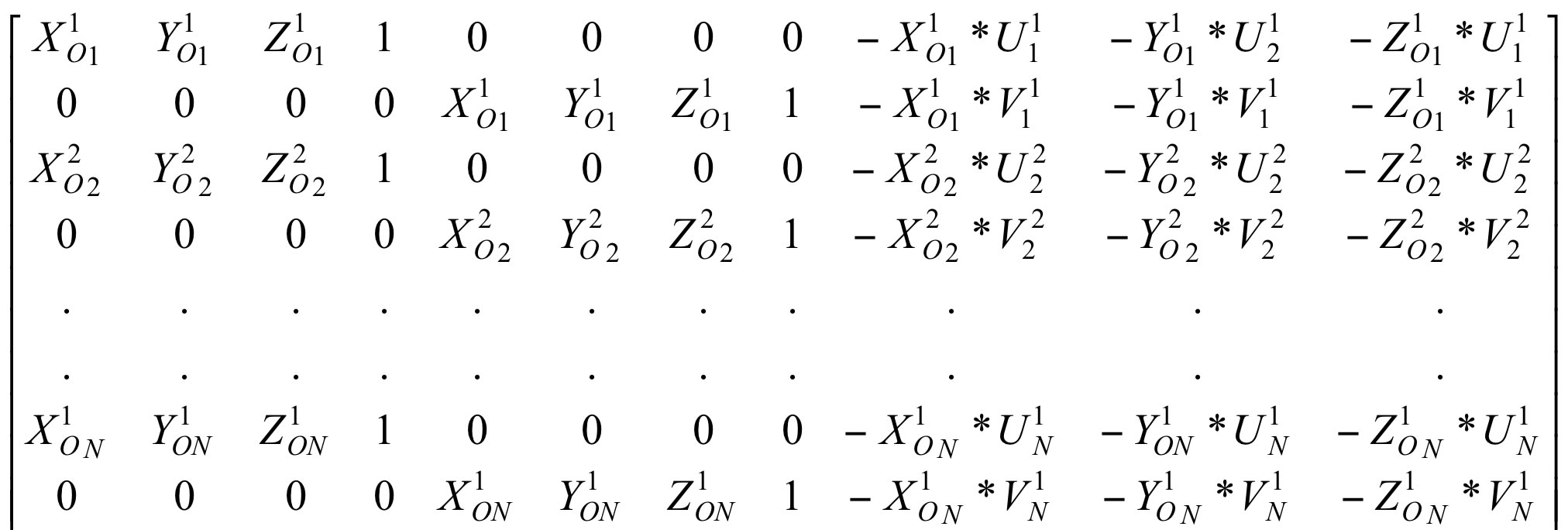
![]() =
=![]()
Рисунок 2 – Связь коэффициентов линейной трансформации ![]() —
—![]() , действительных координат тест-объекта
, действительных координат тест-объекта ![]() и координат тест-объекта в двух плоских снимках
и координат тест-объекта в двух плоских снимках ![]() , верхние индексы i=1,2 – относятся к камерам; нижние индексы j относятся к меткам на тест-объекте
, верхние индексы i=1,2 – относятся к камерам; нижние индексы j относятся к меткам на тест-объекте
- минимальное количество меток на тест-объекте 6;
- тест-объект должен перекрывать предполагаемое пространство локомоций с целью избежания необходимости экстраполировать калибровочные коэффициенты
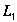 —
—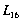 на пространство большее размеров тест-объекта;
на пространство большее размеров тест-объекта; - после калибровки нельзя передвигать камеры;
- точки должны лежать в трех плоскостях;
- тест-объект (или одну из его сторон) выставлять строго вертикально, например, по отвесу;
- оптимальное отношение расстояний между камерами и объектом съемки 1 к 2.
